Graphs
Graphs in SeqAn.
 |
Graphs can be used to model a great variety of problems and hence,
they are in widespread use as a problem-solving tool. Directed and undirected graphs, trees, automatons, and
alignment graphs are different types of graphs with distinct features. In SeqAn, all graph types
are specializations of Graph. Graphs can be traversed using iterators. Besides the fundamental
graph data structures, SeqAn provides the most well-known graph algorithms, e.g. Dijkstra's shortest
path algorithm. The fundamental graph algorithms are supplemented with some specialized alignment algorithms.
All graphs can be exported in dot format for visualization.
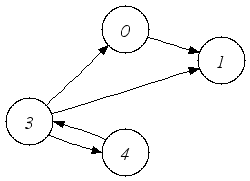 |
| A directed graph. |
A Directed graph expects 2 optional arguments, a cargo and a specification.
Cargos are attached to edges in the graph. A typical example are distances for flight networks represented as a graph.
The basic principle is simple: If you add an edge you have to provide a cargo,
if you remove an edge you also remove the cargo. If you do not want to use cargos, you
can leave out the TCargo parameter or you can use void , which is the default.
All edges are directed that is, they have a distinct source
and target vertex.
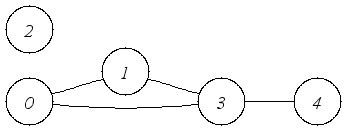 |
| An undirected graph with multiple components. |
An Undirected graph has, of course, undirected edges but in all other respects,
it can be used in the same way as a directed graph.
In this example, the edges have no cargo.
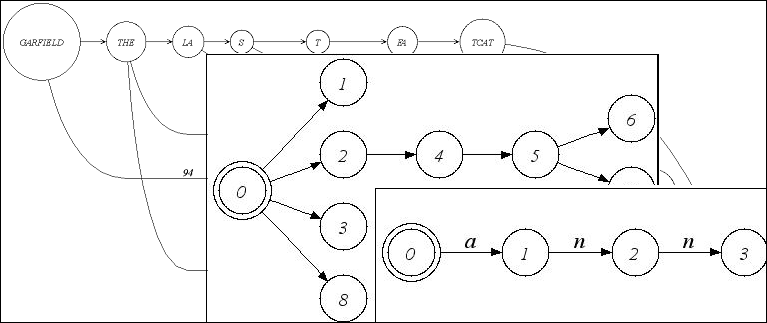 |
| Alignment graph, tree, and trie. |
SeqAn is not a new library for graph data structures and algorithms. It focusses on sequence analysis.
Hence we introduced graphs as helper classes for string matching or alignment algorithms.
Besides directed and undirected graphs, those algorithms make use of special graphs
like a Tree, an Automaton, a Trie or an Alignment Graph.
These graphs are therefore predefined in SeqAn.
All graphs support a couple of common functions, including numEdges, numVertices,
addVertex, removeVertex, addEdge etc. The functions are listed and explained in the Graph
section but the function names should be self-explanatory. Besides this core set of function, some graphs
have special methods, e.g., trees support childVertex, addChild, and the like. See the documentation
of these graphs for details. The following code snippet illustrates the use of these functions to create the directed
graph in the first figure.
TVertexDescriptor v0 = addVertex(g);
TVertexDescriptor v1 = addVertex(g);
TEdgeDescriptor e1 =addEdge(g,v0,v1);
TVertexDescriptor v2 = addVertex(g);
TVertexDescriptor v3 = addVertex(g);
TVertexDescriptor v4 = addVertex(g);
addEdge(g,v3,v4);
addEdge(g,v3,v0);
addEdge(g,v3,v1);
addEdge(g,v4,v3);
removeVertex(g, v2);
As you can see in this example, all vertices are represented by vertex descriptors and all edges are represented
by edge descriptors. Both types can be accessed by the corresponding metafunction, namely VertexDescriptor
and EdgeDescriptor. Vertex and edge descriptors are the value types of all iterators working
on graphs.
Iterators are used to traverse a graph. The value of vertex and edge iterators always
returns a vertex or edge descriptor, respectively. These descriptors are a kind of handle to deal with vertices and edges, e.g. an
edge descriptor can be used to access the cargo of an edge. Vertex Iterator, Adjacency Iterator,
Bfs Iterator and Dfs Preorder Iterator are the basic vertex iterators. Exemplary, the following
code snippet shows how the adjacency iterator is initialized on vertex 3 and then traverses all
the adjacent neighbors.
TAdjacencyIterator it(g,3);
for(;!atEnd(it);goNext(it)) {
std::cout << *it << std::endl;
}
In this example, you can see how the metafunction Iterator is used to get the correct iterator
type for TGraph . We simply output all adjacent vertices. In respect to edge iterators, SeqAn provides a simple Edge Iterator
and an Out-Edge Iterator. The use of the latter is showed in the next figure.
TOutEdgeIterator it(g, v0);
for(;!atEnd(it);goNext(it)) {
std::cout << cargo(*it) << std::endl;
}
In this example, we traverse all out-edges of vertex 0 and print their cargo.
Property maps are a fundamental abstraction mechanism to attach auxiliary information to the vertices and
edges of a graph. A typical example are the city names and flight distances of a graph representing
a flight network. In most scenarios, users should use an external property map to attach this information
to the graph but other mechanisms do exist (e.g., the possibility to use a Cargo).
Be aware that the word external is a hint that the information is stored independent of the graph
and functions like removeVertex do not affect the property map. Property maps are indexed
via the already well-known vertex and edge descriptors. This is quite handy since we can use, for instance, a
vertex iterator to traverse the graph and access the properties on the fly. Most graph algorithms
make heavily use of this concept and therefore it is illustrated below.
First, let us create a simple graph.
TVertexDescriptor v0 = addVertex(g);
TVertexDescriptor v1 = addVertex(g);
TEdgeDescriptor e1 =addEdge(g,v0,v1);
Second, we have to create and resize an edge property map so that it can hold information on all edges.
resizeEdgeMap(g , distanceMap);
As you can see, property maps are simply strings of some type. In this case, we use unsigned integer to
store the distances for our graph g . For each edge we can store a distance now.
Note how the edge descriptor is used to access the property map. An algorithm can now traverse
all edges and access the distances.
TEdgeIterator it(g);
for(;!atEnd(it);goNext(it)) {
std::cout << getProperty(distanceMap, *it) << std::endl;
}
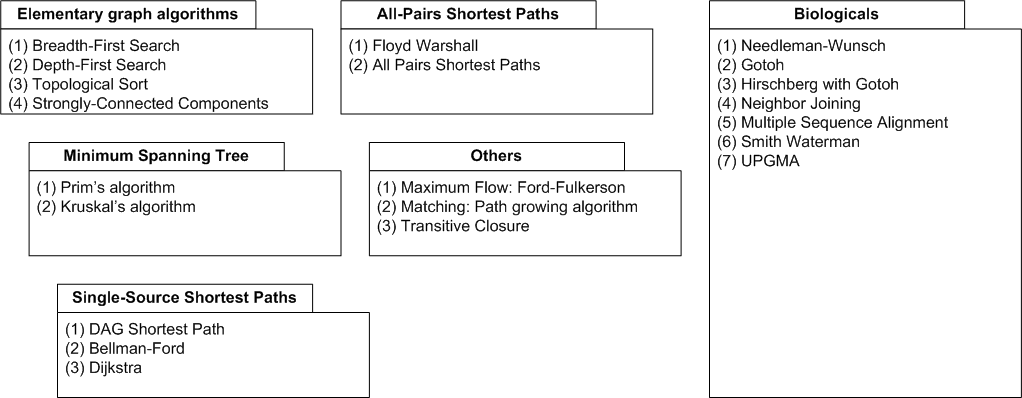 |
| Graph algorithms. |
The above figure gives an overview of the graph algorithms currently available in SeqAn. The biological algorithms
use heavily the alignment graph, all others use the appropriate standard graph. All algorithm require some kind
of additional input, e.g., the Dijkstra algorithm requires a distance map, alignment algorithms sequences and a score
type, or the network flow algorithm capacities on edges. The basic usage can be found in the documentation but
a simple example is given here. The following code snippet aligns two sequences.
typedef StringSet<TString, Dependent<> > TStringSet;
typedef Graph<Alignment<TStringSet, void> > TGraph;
TStringSet str;
TString str0("annual");
assignValueById(str, str0);
TString str1("annealing");
assignValueById(str, str1);
TGraph g(str);
Score<int> score_type = Score<int>(0,-1,-1,0);
int score = globalAlignment(g, score_type, NeedlemanWunsch() );
We first assign the sequences annual and annealing to a string set.
Based on this string set an alignment graph is created. A score object is
used to configure the Needleman Wunsch algorithm and the globalAlignment call
creates the alignment.
SeqAn - Sequence Analysis Library - www.seqan.de