Indices
Substring indices in SeqAn.
 |
A substring index is a datatype which allows to seek efficiently for all occurrences of a pattern
in a string or a set of strings.
Substring indices are very efficient for the exact string matching problem, i.e. finding all exact occurrences of a pattern in a text or a text collection.
Instead of searching through the text in O(n) like online-search algorithms do, a substring index looks up the pattern in sublinear time o(n).
Substring indices are full-text indices, i.e. they handle all substrings of a text in contrast to inverted files or signature files, which need word delimiters.
SeqAn contains data structures to create, hold and use substring indices.
Based on a unified concept, SeqAn offers several concrete implementations (e.g. enhanced suffix array, lazy suffix tree,
q-gram index, nested q-gram index, etc.) defined as specializations of Index.
The unified concept allows every index (except the simple q-gram index) to be accessed just like a suffix tree independently of its concrete implementation.
To access this (virtual) suffix tree SeqAn offers various iterators.
A substring index is a specialization of the generic class Index which expects 2 arguments (the second is optional).
The first template argument is the type of the data structure the index should be built on.
In the following, we denote this type by TText .
For example, this could be String<char> to create a substring index on a string of characters:
or StringSet<String<char> > to create an index on a set of character strings:
The second template argument of the Index class specifies the concrete implementation.
In the following, we denote this type by TSpec .
By default, this is Index_ESA<> to use an enhanced suffix array.
So, our first code example could also be written as:
After we have seen how to instantiate an index object, we need to know how to assign a sequence the index should be built on.
This can be done with the function indexText which returns a reference to a TText object stored in the index or
directly with the index constructor:
Index< String<char> > myIndex;
indexText(myIndex) = "tobeornottobe";
// ... could also be written as
Index< String<char> > myIndex("tobeornottobe");
To find all occurrences of a pattern in an indexed String or a StringSet, SeqAn provides the Finder class (see searching tutorial),
which is also specialized for indices.
The following example shows, how to use the Finder class specialized for our index to search the pattern "be" .
while (find(myFinder, "be"))
cout << position(myFinder) << " ";
The finder object myFinder was created with a reference to myIndex .
The function find searches the next occurence of "be" and returns true if an occurrence was found and false after all occurrences have been passed.
The positition of an occurrence in the text is returned by the function position called with the Finder object.
Please note that in contrast to online-search algorithms (see searching tutorial) the returned occurrence positions are not ascending.
As you can see in the code example above, the pattern "be" was passed directly to the function find function.
This is a shortcut for indices and could be also written in a longer way (already known from the searching tutorial):
Pattern< String<char> > myPattern("be");
while (find(myFinder, myPattern))
cout << position(myFinder) << " ";
We consider an alphabet Σ and a sentinel character $ that is smaller than every character of Σ.
A suffix tree of a given non-empty string s over Σ is a directed tree whose edges are labeled with non-empty substrings of s $ with the following properties:
1. Each outgoing edge begins with a different letter and the outdegree of an internal node is greater than 1.
2. Each suffix of s $ is the concatenation of edges from the root to a leaf node.
3. Each path from the root to a leaf node is a suffix of s $ .
The following figure shows the suffix tree of the string s="mississippi" (suffix nodes are shaded):
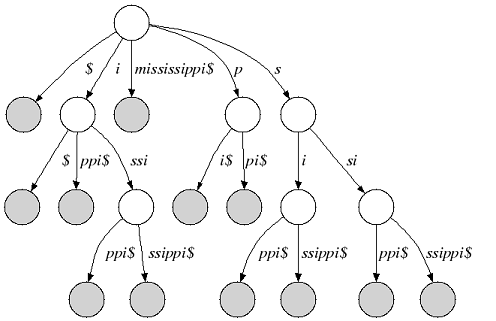 |
| Suffix tree of |
Many suffix tree construction algorithms expect $ to be part of the string alphabet which is undesirable for small bit-compressible alphabets (e.g. DNA).
In SeqAn there is no need to introduce a $. We relax suffix tree criteria 2. and consider the relaxed suffix tree that arises from the suffix tree of s by removing the $ character and all empty edges.
In the following, we only consider relaxed suffix trees and simply call them suffix trees.
In that tree a suffix can end in an inner node as you can see in the next figure (suffix i ):
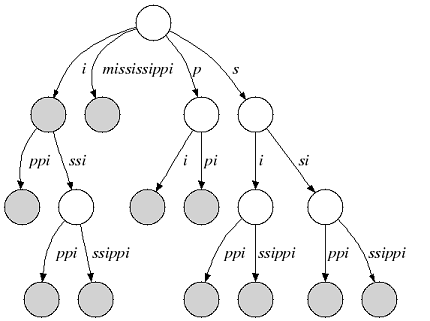 |
| Relaxed suffix tree of |
In SeqAn a suffix tree can be accessed with special suffix tree iterators, which differ in the way the tree nodes are traversed.
For a lot of sequence algorithms it is neccessary to do a full depth-first search (dfs) over all suffix tree nodes beginning either in the root (preorder dfs) or in a leaf node (postorder dfs).
A preorder traversal halts in a node when visiting it for the first time whereas a postorder traversal halts when visiting a node for the last time.
The following two figures give an example in which order the tree nodes are visited:
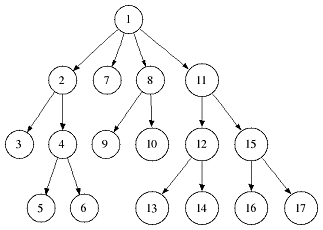 | 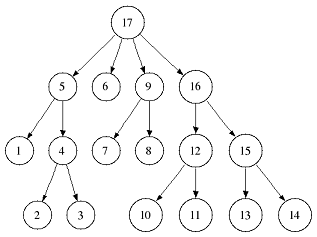 |
| Preorder dfs traversal | Postorder dfs traversal |
A postorder traversal, also known as bottom-up traversal, can be realized with the BottomUp Iterator.
This iterator starts in the left-most (lexicographically smallest) leaf and provides the functions goNext, atEnd, and goBegin
to proceed with the next node in postorder, to test for having been visiting all nodes, and to go back to the first node of the traversal.
The BottomUp Iterator can be optained by the Iterator meta-function called with an Index type and the BottomUp specialization type.
The following example shows how our index can be traversed as a suffix tree with myIterator in a bottom-up fashion:
Iterator< Index<String<char> >, BottomUp<> >::Type myIterator(myIndex);
for (; !atEnd(myIterator); goNext(myIterator))
// do something with myIterator
Another kind of traversing the suffix tree provides the light-weight TopDown Iterator.
Starting in the root node the iterator can goDown the left-most edge, the edge beginning with a certain character or the path of a certain string.
goRight can be used to go to the right (lexicographically larger) sibling of the current node.
These functions return a bool which indicates whether the iterator could successfully be moved.
To visit the children of the root node in lexicographical ascending order you could write:
goDown(myIterator);
while (goRight(myIterator))
// do something with myIterator
To go back to upper nodes you can either save copies of the TopDown Iterator or use the heavier TopDownHistory Iterator which stores the way back to the root and can goUp.
This is a specialization of the TopDown Iterator and can be instantiated with Iterator< Index<String<char> >, TopDown<ParentLink<> > >::Type myIterator(myIndex); .
As this iterator can randomly walk through the suffix tree it can easily be used to do a preorder or postorder dfs.
Therefore this iterator also implements the functions goNext and atEnd.
The order of the dfs traversal can be specified with an optional template argument of ParentLink<..> which can be Preorder (default) ...
Iterator< Index<String<char> >, TopDown<ParentLink<Preorder> > >::Type myIterator(myIndex);
for (; !atEnd(myIterator); goNext(myIterator))
// do something with myIterator
... or Postorder. As top-down iterators starts in the root node, the iterator must manually be moved down to the first postorder node which is the left-most leaf:
Iterator< Index<String<char> >, TopDown<ParentLink<Postorder> > >::Type myIterator(myIndex);
while (goDown(myIterator));
for (; !atEnd(myIterator); goNext(myIterator))
// do something with myIterator
Note:
A relaxed suffix tree is a suffix tree after removing the $ characters and empty edges.
For some bottom-up algorithms it would be better not to remove empty edges and to have a one-to-one relationship between leaves and suffices.
In that cases you can use the tags PreorderEmptyEdges or PostorderEmptyEdges instead of Preorder or Postorder or
EmptyEdges for the TopDown Iterator.
In the previous subsection we have seen how to walk through a suffix tree.
We now want to know what can be done with a suffix tree iterator.
As all iterators are specializations of the general VSTree Iterator class, they inherit all of its functions.
There are various functions to access the node the iterator points at, so we concentrate on the most important ones.
| representative | returns the substring that represents the current node, i.e. the concatenation of substrings on the path from the root to the current node |
| getOccurrence | returns a position where the representative occurs in the text |
| getOccurrences | returns a string of all positions where the representative occurs in the text |
| isRightTerminal | tests if the representative is a suffix in the text (corresponds to the shaded nodes in the figures above) |
| isLeaf | tests if the current node is a tree leaf |
| parentEdgeLabel | returns the substring that represents the edge from the current node to its parent (only TopDownHistory Iterator) |
Note:
There is a difference between the functions isLeaf and isRightTerminal.
In a relaxed suffix tree a leaf is always a suffix, but not vice versa, as there can be internal nodes a suffix ends in.
For them isLeaf returns false and isRightTerminal returns true.
By now, we know the following iterators (n=text size, σ=alphabet size, d=tree depth):
| BottomUp Iterator | postorder dfs | O(d) | SA, LCP |
| TopDown Iterator | can go down and go right | O(1) | SA, LCP, ChildTab |
| TopDownHistory Iterator | can also go up, preorder/postorder dfs | O(d) | SA, LCP, ChildTab |
Besides the iterators described above, there are some application-specific iterators in SeqAn:
| MaxRepeats Iterator | maximal repeats | O(n) | SA, LCP, BWT |
| SuperMaxRepeats Iterator | supermaximal repeats | O(d+σ) | SA, LCP, ChildTab, BWT |
| SuperMaxRepeatsFast Iterator | supermaximal repeats (optimized for enh. suffix arrays) | O(σ) | SA, LCP, BWT |
| MUMs Iterator | maximal unique matches | O(d) | SA, LCP, BWT |
| MultiMEMs Iterator | multiple maximal exact matches (w.i.p.) | O(n) | SA, LCP, BWT |
Given a string s a repeat is a substring r that occurs at 2 different positions i and j in s .
The repeat can also be identified by the triple (i,j,|r|) .
A maximal repeat is a repeat that cannot be extended to the left or to the right, i.e. s[i-1]≠s[j-1] and s[i+|r|]≠s[j+|r|] .
A supermaximal repeat r is a maximal repeat that is not part of another repeat.
Given a set of strings s1 , ..., sm a MultiMEM (multiple maximal exact match) is a substring r that occurs in each sequence si
at least once and cannot be extended to the left or to the right right.
A MUM (maximal unique match) is a MultiMEM that occurs exactly once in each sequence.
The following examples demonstrate the usage of these iterators:
| Maximal Unique Matches |
| Supermaximal Repeats |
| Maximal Repeats |
Section 1 briefly described how an index of a set of strings can be instantiated.
Instead of creating an Index of a String you create one of a StringSet.
A character position of this string set can be one of the following:
1. A local position (default), i.e. Pair (seqNo, seqOfs) where seqNo identifies the string within the stringset
and the seqOfs identifies the position within this string.
2. A global position, i.e. single integer value between 0 and the sum of string lengths minus 1 (global position).
This integer is the position in the gapless concatenation of all strings in the StringSet to a single string.
The meta-function SAValue determines, which position type (local or global) will be used for internal
index tables (suffix array, q-gram array) and what type of position is returned by function like getOccurrence
or position of a Finder. SAValue returns a Pair=local position by default,
but could be specialized to return an integer type=global position for some applications.
If you want to write algorithms for both variants you should use the functions posLocalize, posGlobalize, getSeqNo and getSeqOffset.
To search in multiple strings the Finder example from above can be modified to:
StringSet< String<char> > mySet;
resize(mySet, 3);
mySet[0] = "tobeornottobe";
mySet[1] = "thebeeonthecomb";
mySet[2] = "beingjohnmalkovich";
// find "be" in Index of StringSet
Index< StringSet<String<char> > > myIndex(mySet);
Finder< Index<StringSet<String<char> > > > myFinder(myIndex);
while (find(myFinder, "be"))
cout << position(myFinder) << " ";
As TText is a StringSet, position(finder) returns a Pair (seqNo,seqOfs) where seqNo is the number and seqOfs the local position of the sequence the pattern occurs at.
Click here to see the complete source code of this example.
The following index implementations are currently part of SeqAn:
| Index_ESA | Enhanced suffix array | Kurtz et al., "Replacing Suffix Trees with Enhanced Suffix Arrays", 2004 |
| Index_Wotd | Lazy suffix tree (work in progress) | Giegerich et al., "Efficient Implementation of Lazy Suffix Trees", 2003 |
| Index_QGram | Simple q-gram index (aka k-mer index) | |
| Index_QGram_Nested | Nested q-gram index (work in progress) |
A simple example for specializing a suffix array based index and a q-gram index for the same pattern matching problem the Index Finder demo.
SeqAn - Sequence Analysis Library - www.seqan.de