Motivation

A compact data structure maintains data, and the desired extra data structures over it, in a form that not only uses less space than usual, but is able to access and query the data in compact form, that is, without decompressing them. Thus, a compact data structure allows us to fit and efficiently query, navigate, and manipulate much larger datasets in main memory than what would be possible if we used the data represented in plain form and classical data structures on top.

A good source of reading (which is online available for free): Gonzalo Navarro, Compact Data Structures

Bitvectors

Bitvectors are fundamental in the implementation of most compact data structures because of their compactness. For example, they can be used to mark positions of an array or to encode and compress data. Therefore, an efficient implementation is of utmost importance.

A bitvector is a bit array 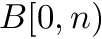of length 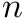of values 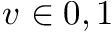$v \in {0,1}$ (bits).

In C++ there is no type that defines a single bit, such that you could use std::vector<bit> for this purpose. If you would use, let's say, std::vector<bool> instead, you would use 1 byte = 8 bit for each entry (note that many compilers actually optimize this special case to indeed a single bit representation but let's assume we want a global solution), or even worse std::vector<int> which uses 4 byte = 32 bit.

Let us design a compact data structure that stores single bits as values while still supporting the basic operations:

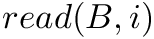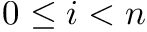: returns the bit , for any $0 \leq i < n$ in constant time.
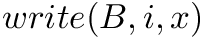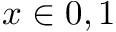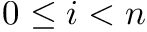: writes the bit $x \in {0,1}$ to , for any $0 \leq i < n$ in constant time.

A compact representation of bitvectors

As noted above we need to represent bits using larger entities available in the C++ language. It usually pays off if you choose an integer with the size of a machine word 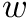, which is 64 on modern architectures, because most compilers offer a special set of functions for integers of this size. Therefore, we will use the C++ type uint64_t for our representation. In the previous sections we talked about arrays of bits, as in a consecutive storage of bits. In C++ we will the use type std::vector for storing values.

A compact bitvector

Implement a new data structure (a struct) called Bitvector that has a member variable called data of type std::vector over uint64_t. The constructor should have one parameter that is the number of bits you would like to store in your bitvector.

If you are inexperienced with C++, take a look at this code snippet and fill in the TODO:

Hint

#include <cinttypes>
#include <vector>
 
struct Bitvector // the new data structure
{
    std::vector<uint64_t> data; // the data storage (64 bit integers instead of single bits)
 
    // The constructor takes one parameter as input called 'count' which is the number of bits you want to store.
    // Your data vector now needs to be resized to store these bits.
    Bitvector(size_t const count)
    {
        data.resize(/*TODO: How many integers do you need to represent `count` bits?*/);
    }
};
 
int main()
{
    Bitvector B(10); // construct an instance B of type Bitvector that can store at least 10 bits
}

Solution

#include <cinttypes>
#include <vector>
 
struct Bitvector
{
    std::vector<uint64_t> data;
 
    Bitvector(size_t const count)
    {
        data.resize((count + 63) / 64); // the +63 is a trick to round up the fraction.
    }
};
 
int main()
{
    Bitvector B(10);
}

Access the compact bitvector

The bitvector needs to support access to the single bits via a member function read(i), which returns either 0 or 1 depending on the bit at position i.

We now face the problem that we do not store single bits but groups of 64 bits in one uint64_t integer. For example, let a data vector contain the number 17.

The 64 bit binary representation of 17 is

0 8 16 24 32 40 48 56

0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0001 0001

It thus represents a group of 64 bits where the bits at position 59 and 63 (starting from the left and 0) are set to 1.

So how do we access single bits within the integer? This can be achieved using bit manipulation.

Read up on basic bit manipulation mechanisms in this tutorial if you are new to this.

Reading

Copy and paste the following implementation of a function into your Bitvector struct and complete the code:

bool read(size_t const i) const
{
    // manipulate the bits of the correct entry to identify whether position i is set to 0 or 1
    // return true if the bit at position i is set to 1 and false otherwise.
}

Your function should be able to access the bitvector in constant time (don't use loops)!

Given the following main function

int main()
{
    Bitvector B(10);
 
    std::cout << B.read(2) << '\n'; // prints 0
}

Your program should output

0

If you are inexperienced with C++, use the provided code snippet of the read function and fill in the TODOs:

Hint

struct Bitvector
{
    std::vector<uint64_t> data;
 
    Bitvector(size_t const count)
    {
        data.resize((count + 63) / 64); // the +63 is a trick to round up the fraction.
    }
 
    bool read(size_t const i) const
    {
        // We need to find the correct group for bit i.
        // For example, if i is 10 it will be the 10th bit in the first 64 bit-group,
        // if i is 70 it will be the 6th bit in the second.
        size_t group_index = /*TODO: In which data entry (group) can we find bit i?*/;
 
        // Now that we identified the correct entry. We need to know the relative position of i within its group,
        // e.g. for i == 70, the group_index is 1 (second group starting with 0) and the relative position x is 6.
        size_t x = /*TODO: what is the relative position of bit i?*/;
 
        // Now that we identified the correct entry and relative position,
        // we need to move the bit of interest to the right most position in order to look at it.
        // This can be done using a right shift of (63 - x) positions.
        // If the then use the logical AND operator with 1 (bit representation 0..01)
        // we set every bit but the last to zero, so we have either 0..0 or 0..1 which is either false or true.
        return (data[group_index] >> (63 - x)) & 1;
    }
};

Solution

#include <iostream>
#include <vector>
 
struct Bitvector
{
    std::vector<uint64_t> data;
 
    Bitvector(size_t const count)
    {
        data.resize((count + 63) / 64); // the +63 are a trick to round up the fraction.
    }
 
    bool read(size_t const i) const
    {
        return (data[i / 64] >> (63 - (i % 64))) & 1;
    }
};
 
int main()
{
    Bitvector B(10);
 
    std::cout << B.read(2) << '\n'; // prints 0
}

Write to the compact bitvector

We now want to support writing to our bitvector by implementing the member function write(i, x). This is a bit more tricky so we recommend this as a bonus question for experienced C++ users. Otherwise you may just copy and paste the solution.

Writing

Complete the following implementation of a function that can access the compact bitvector:

void write(size_t const i, bool const x)
{
    // ... your implementation goes here
}

Solution

#include <iostream>
#include <vector>
 
struct Bitvector
{
    std::vector<uint64_t> data;
 
    Bitvector(size_t const count)
    {
        data.resize((count + 63) / 64); // the +63 are a trick to round up the fraction.
    }
 
    bool read(size_t const i) const
    {
        return (data[i / 64] >> (63 - (i % 64))) & 1;
    }
 
    void write(size_t const i, bool const value)
    {
        uint64_t mask = static_cast<uint64_t>(1) << (63 - (i % 64));
 
        if (value == true)
            data[i / 64] |= mask;
        else
            data[i / 64] &= ~mask;
    }
};
 
int main()
{
    Bitvector B(10);
 
    std::cout << B.read(63) << '\n'; // prints 0
    B.write(63, 1);                       // writes a 1 at position 63 in the bitvector
    std::cout << B.read(63) << '\n'; // prints 1
    B.write(63, 0);                       // writes a 0 at position 63 in the bitvector
    std::cout << B.read(63) << '\n'; // prints 0 again
}

Rank and select

Two very useful operations that a bitvector should support are the following:

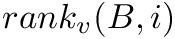: returns the number of occurrences of bit 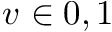$v \in {0, 1}$ in 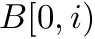, for any 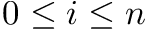$0 \leq i \leq n$ . If omitted, we assume .
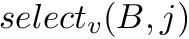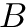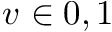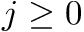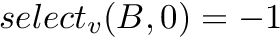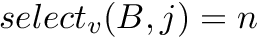: returns the position in of the j-th occurrence of bit $v \in {0, 1}$ , for any $j \geq 0$ ; we assume and if 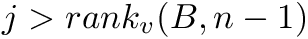. If omitted, we assume .

We will implement the rank operation for our compact bitvector representation.

Helper data structures

In order to support rank and select queries we need two helper data structures (given machine world length ):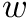

Superblocks: We divide the bitvector into superblocks of length 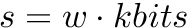$s = w \cdot k bits$ , where 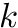is parameter to choose. We then store the rank values at the beginnings of the corresponding superblock in an array .
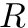Blocks: We further divide the bitvector into blocks of length 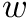. We then store the rank values at the beginnings of the corresponding block, but relatively to their corresponding superblock, in an array .

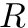Data types

The block and superblock values obviously need to be stored using an arithmetic data type (e.g. uint8_t, uint16_t, uint32_t, uint64_t). Given an arbitrary bitvector of length n, word length 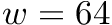bits and a superblock length of 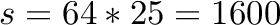bits, which type would you choose for superblock entries, and which type for block entries and why?

Solution

If a superblock spans 1600 bits, then the last block value within a superblock can at most count 1599 1s. Thus, a uint16_t is the smallest type that is still able represent this number and should be preferred to larger types to reduce the space of the block data structure.

Since we do not know how large our bitvector might be, one should choose a large data type, like uint64_t, to store to prefix sums for the superblock values.

Now that we know which data types to work with, let's implement the data structures.

Compute the block and superblock arrays

Given a bitvector B from the previous assignments:

Add the member variables std::vector<uint16_t> blocks and std::vector<uint64_t> superblocks.
Add the member variables uint16_t block_size and uint16_t superblock_size.
Add a member function void construct(size_t const new_block_size = 64, size_t const new_superblock_size = 512) that overwrites the member variables block_size and superblock_size and then fills the member variables blocks and superblocks.

With the following main function:

int main()
{
    Bitvector B(6400);
 
    for (size_t i = 0; i < 100; ++i)
        B.write(i * 64, 1);
 
    B.construct(64, 1600);
 
    std::cout << "Superblocks:" << '\n';
    for (auto a : B.superblocks)
        std::cout << a << " ";
    std::cout << '\n' << '\n';
 
    std::cout << "Blocks:" << '\n';
    for (auto a : B.blocks)
        std::cout << a << " ";
    std::cout << '\n';
}

your program should print the following:

Superblocks:
25 50 75
 
Blocks:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24

If you are inexperienced with C++, you can use the following code snippet and fill in the TODOs:

Hint

// The member function takes two parameters:
// `block_size` which is defaulted to be 64 and `superblock_size` which is defaulted to 512.
// Defaulted means that you can also call the function without parameters `construct()`.
void construct(size_t const new_block_size = 64, size_t const new_superblock_size = 512)
{
    block_size = new_block_size;            // overwrite the member variable with the new value
    superblock_size = new_superblock_size;  // overwrite the member variable with the new value
 
    size_t number_of_bits = data.size() * 64;
 
    // resize the two arrays of blocks and superblocks
    blocks.resize(/*TODO: how many blocks do I need?*/);
    superblocks.resize(/*TODO: how many super blocks do I need?*/);
 
    // keep track of the current (super)block
    size_t block_pos{0};
    size_t super_block_pos{0};
 
    // keep track of the current (super)block count value
    uint16_t block_count{0};
    uint64_t super_block_count{0};
 
    // iterate over the data member and count the number of 1's.
    for (size_t i = 0; i < number_of_bits; ++i)
    {
        if (/*TODO: When do we reach the end of a block? Hint: Use the modulo operation (%) on i*/)
        {
            if (/*TODO: When do we reach the end of a superblock? Hint: Use the modulo operation (%) on i*/)
            {
                super_block_count += block_count; // update superblock count
 
                // TODO: store the value of super_block_count into the current superblock entry (at super_block_pos)
 
                ++super_block_pos; // move to the next position
                block_count = 0;   // reset block count
            }
 
            // TODO: store value of block_count in the current block entry (at super_block_pos)
 
            ++block_pos; // move to the next position
        }
 
        if (read(i) == true)
            ++block_count;
    }
}

Solution

#include <iostream>
#include <vector>
 
struct Bitvector
{
    std::vector<uint64_t> data;
    std::vector<uint16_t> blocks;
    std::vector<uint64_t> superblocks;
 
    uint64_t block_size;
    uint64_t superblock_size;
 
    Bitvector(size_t const count)
    {
        data.resize((count + 63) / 64); // the +63 are a trick to round up the fraction.
    }
 
    bool read(size_t const i) const
    {
        return (data[i / 64] >> (63 - (i % 64))) & 1;
    }
 
    void write(size_t const i, bool const value)
    {
        uint64_t mask = static_cast<uint64_t>(1) << (63 - (i % 64));
 
        if (value == true)
            data[i / 64] |= mask;
        else
            data[i / 64] &= ~mask;
    }
 
    void construct(size_t const new_block_size = 64, size_t const new_superblock_size = 512)
    {
        block_size = new_block_size;
        superblock_size = new_superblock_size;
 
        size_t number_of_bits = data.size() * 64;
 
        blocks.resize((number_of_bits + block_size - 1) / block_size, 0);
        superblocks.resize((number_of_bits + superblock_size - 1) / superblock_size, 0);
 
        size_t block_pos{0};
        size_t super_block_pos{0};
 
        uint16_t block_count{0};
        uint64_t super_block_count{0};
 
        for (size_t i = 0; i < number_of_bits; ++i)
        {
            if (i % block_size == 0)
            {
                if (i % superblock_size == 0)
                {
                    super_block_count += block_count; // update superblock count
 
                    superblocks[super_block_pos] = super_block_count;
 
                    ++super_block_pos; // move to the next position
                    block_count = 0;   // reset block count
                }
 
                blocks[block_pos] = block_count;
 
                ++block_pos; // move to the next position
            }
 
            if (read(i) == true)
                ++block_count;
        }
    }
};
 
int main()
{
    Bitvector B(6400);
 
    for (size_t i = 0; i < 100; ++i)
        B.write(i * 64, 1);
 
    B.construct(64, 1600);
 
    std::cout << "Superblocks:" << '\n';
    for (auto a : B.superblocks)
        std::cout << a << " ";
    std::cout << '\n' << '\n';
 
    std::cout << "Blocks:" << '\n';
    for (auto a : B.blocks)
        std::cout << a << " ";
    std::cout << '\n';
}

Note that most compilers provide special bit operations on integers. One example is popcount that counts the number of 1s in an integer. This would be very helpful in our application because instead of iterating over every position in our bitvector B we could directly use popcount on every entry of B to get the value for the block (of course this only works since we chose the block size wisely).

The code could then look like this (This is compiler specific (GCC)):

#include <iostream>
#include <vector>
 
struct Bitvector
{
    std::vector<uint64_t> data;
    std::vector<uint16_t> blocks;
    std::vector<uint64_t> superblocks;
 
    uint64_t block_size;
    uint64_t superblock_size;
 
    Bitvector(size_t const count)
    {
        data.resize((count + 63) / 64); // the +63 are a trick to round up the fraction.
    }
 
    bool read(size_t const i) const
    {
        return (data[i / 64] >> (63 - (i % 64))) & 1;
    }
 
    void write(size_t const i, bool const value)
    {
        uint64_t mask = static_cast<uint64_t>(1) << (63 - (i % 64));
 
        if (value == true)
            data[i / 64] |= mask;
        else
            data[i / 64] &= ~mask;
    }
 
    void construct(size_t const new_block_size = 64, size_t const new_superblock_size = 512)
    {
        block_size = new_block_size;
        superblock_size = new_superblock_size;
 
        size_t number_of_bits = data.size() * 64;
 
        blocks.resize((number_of_bits + block_size - 1) / block_size, 0);
        superblocks.resize((number_of_bits + superblock_size - 1) / superblock_size, 0);
 
        size_t block_pos{0};
        size_t super_block_pos{0};
 
        uint16_t block_count{0};
        uint64_t super_block_count{0};
 
        // now we only need to iterate over each 64bit integer because we can count the 1's en bloc
        for (size_t i = 0; i < data.size(); ++i)
        {
            if ((i * 64) % block_size == 0)
            {
                if ((i * 64) % superblock_size == 0)
                {
                    super_block_count += block_count; // update superblock count
 
                    superblocks[super_block_pos] = super_block_count;
 
                    ++super_block_pos; // move to the next position
                    block_count = 0;   // reset block count
                }
 
                blocks[block_pos] = block_count;
 
                ++block_pos; // move to the next position
            }
 
            block_count += __builtin_popcountll(data[i]);
        }
    }
};
 
int main()
{
    Bitvector B(6400);
 
    for (size_t i = 0; i < 100; ++i)
        B.write(i * 64, 1);
 
    B.construct(64, 1600);
 
    for (auto a : B.blocks)
        std::cout << a << " ";
    std::cout << '\n';
 
    for (auto a : B.superblocks)
        std::cout << a << " ";
    std::cout << '\n';
}

If you have some time to spare, increase the size of B, and do some runtime tests for the construction. The construction using popcount should be considerably faster.

Rank queries

Now that we have the helper data structures of block and superblocks, we will implement the actual support for rank queries.

Rank queries

Implement a member function

uint64_t rank(size_t const i) const
{
    // your code here
}

that returns the number of occurrences of bit 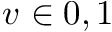$v \in {0, 1}$ in 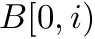, for any 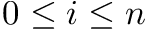$0 \leq i \leq n$ ; in particular 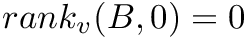. If omitted, we assume .

Use the same example of the bitvector and block/superblock sizes as in the previous assignment.

Given the following main function:

int main()
{
    Bitvector B(6400);
 
    for (size_t i = 0; i < 100; ++i)
        B.write(i * 64, 1);
 
    B.construct(64, 1600);
 
    std::cout << B.rank(1) << '\n';  // 1
    std::cout << B.rank(64) << '\n'; // 1
    std::cout << B.rank(65) << '\n'; // 2
}

Your program should output

1
1
2

If you are inexperienced with C++, you can use the following code snippet:

Hint

uint64_t rank(size_t const i) const
{
    uint64_t rank{0};
 
    rank += superblocks[/*TODO: the position of the superblock entry to use*/];
    rank += blocks[/*TODO: the position of the block entry to use*/];
 
    // go through the remaining block bit-by-bit
    for (size_t j = (i / block_size) * block_size; j < i; ++j)
    {
        /*TODO: increase `rank` by 1 if there is a 1 at position j in data. Hint: Use a function we implemented.*/
    }
    return rank;
}

Solution

Here is the rank function:

    uint64_t rank(size_t const i) const
    {
        uint64_t rank{0};
 
        rank += superblocks[i / superblock_size];
        rank += blocks[i / block_size];
 
        for (size_t j = (i / block_size) * block_size; j < i; ++j)
        {
            rank += read(j);
        }
 
        return rank;
    }

Here is the full solution:

#include <iostream>
#include <vector>
 
struct Bitvector
{
    std::vector<uint64_t> data;
    std::vector<uint16_t> blocks;
    std::vector<uint64_t> superblocks;
 
    uint64_t block_size;
    uint64_t superblock_size;
 
    Bitvector(size_t const count)
    {
        data.resize((count + 63) / 64); // the +63 are a trick to round up the fraction.
    }
 
    bool read(size_t const i) const
    {
        return (data[i / 64] >> (63 - (i % 64))) & 1;
    }
 
    void write(size_t const i, bool const value)
    {
        uint64_t mask = static_cast<uint64_t>(1) << (63 - (i % 64));
 
        if (value == true)
            data[i / 64] |= mask;
        else
            data[i / 64] &= ~mask;
    }
 
    void construct(size_t const new_block_size = 64, size_t const new_superblock_size = 512)
    {
        block_size = new_block_size;
        superblock_size = new_superblock_size;
 
        size_t number_of_bits = data.size() * 64;
 
        blocks.resize((number_of_bits + block_size - 1) / block_size, 0);
        superblocks.resize((number_of_bits + superblock_size - 1) / superblock_size, 0);
 
        size_t block_pos{0};
        size_t super_block_pos{0};
 
        uint16_t block_count{0};
        uint64_t super_block_count{0};
 
        for (size_t i = 0; i < number_of_bits; ++i)
        {
            if (i % block_size == 0)
            {
                if (i % superblock_size == 0)
                {
                    super_block_count += block_count; // update superblock count
 
                    superblocks[super_block_pos] = super_block_count;
 
                    ++super_block_pos; // move to the next position
                    block_count = 0;   // reset block count
                }
 
                blocks[block_pos] = block_count;
 
                ++block_pos; // move to the next position
            }
 
            if (read(i) == true)
                ++block_count;
        }
    }
 
    uint64_t rank(size_t const i) const
    {
        uint64_t rank{0};
 
        rank += superblocks[i / superblock_size];
        rank += blocks[i / block_size];
 
        for (size_t j = (i / block_size) * block_size; j < i; ++j)
        {
            rank += read(j);
        }
 
        return rank;
    }
};
 
int main()
{
    Bitvector B(6400);
 
    for (size_t i = 0; i < 100; ++i)
        B.write(i * 64, 1);
 
    B.construct(64, 1600);
 
    std::cout << B.rank(1) << '\n';  // 1
    std::cout << B.rank(64) << '\n'; // 1
    std::cout << B.rank(65) << '\n'; // 2
}

Difficulty	Easy
Duration	120 min
Prerequisite tutorials
Recommended reading	Compact Data Structures (Navarro)

Table of Contents

Motivation

Bitvectors

A compact representation of bitvectors

A compact bitvector

Access the compact bitvector

Reading

Write to the compact bitvector

Writing

Rank and select

Helper data structures

Data types

Compute the block and superblock arrays

Rank queries

Rank queries