Motivation

In 1994, Burrows and Wheeler proposed a lossless compression algorithm (now used in bzip2). The algorithm transforms a given text into the so called Burrows-Wheeler transform (BWT), a permutation of the text that can be reversed. In general, the transformed text can be compressed better than the original text as in the BWT equal characters tend to form consecutive runs which can be compressed using run-length encoders.

We will see that it is possible to conduct exact searches using only the BWT and some auxiliary tables.

Theoretical Background: Burrows-Wheeler transform and LF-Mapping

The Burrows-Wheeler transform (BWT) of a text 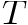ending with a special character 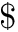$\$$ can be obtained by the following steps:

Form a conceptual matrix 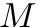whose rows are the 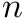cyclic shifts of the text .
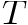Lexicographically sort the rows of .
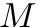Construct the transformed text 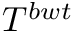$T^{bwt}$ by taking the last column 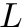of .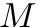

Instead of actually constructing the huge matrix, we can also construct the suffix array in 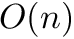time and space, and then construct the BWT from that:

$T^{bwt}[i]=\begin{cases} ~T[A[i]-1] & \text{ if } A[i]>0 \\ ~\$ & \text{ else } \end{cases}$

One interesting property of the Burrows-Wheeler transform 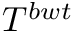$T^{bwt}$ is that the original text 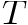can be reconstructed by a reverse transform without any extra information. Therefor, we need the following definition:

Definition (L-to-F mapping): Let 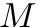be the sorted matrix of cyclic shifts of the text 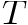. 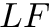is a function 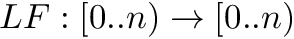$LF : [0..n) \rightarrow [0..n)$ that maps the rank of a cyclic shift 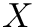to the rank of 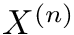$X^{(n)}$ , i.e 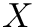shifted by one to the right:

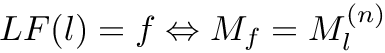
$LF(l) = f \Leftrightarrow M_f = M_l^{(n)}$

This property is the key when searching in the BWT.

In order to conduct the LF-Mapping efficiently, we need two helper data structures, namely the occurence table 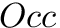and the count table .

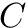Helper data structures: Occ & C

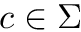Let $C : \Sigma \rightarrow [0..n]$ be a function that maps a character $c \in \Sigma$ to the total number of occurrences in 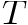of the characters which are alphabetically smaller than .

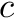Implement the count table

Use this code to construct a BWT from a given input text:

#include <algorithm>
#include <iostream>
#include <numeric>
#include <string>
#include <vector>
 
std::string bwt_construction(std::string const & text)
{
    std::string bwt{};
 
    std::vector<uint64_t> sa(text.size() + 1);
    std::iota(sa.begin(), sa.end(), 0);
    std::sort(sa.begin(), sa.end(), [&text](uint64_t a, uint64_t b) -> bool
    {
        while (a < text.size() && b < text.size() && text[a] == text[b])
        {
            ++a, ++b;
        }
 
        if (b == text.size())
            return false;
 
        if (a == text.size())
            return true;
 
        return text[a] < text[b];
    });
 
    for (auto x : sa)
    {
        if (!x)
            bwt += "$";
        else
            bwt += text[x-1];
    }
 
    return bwt;
}

For simplicity, we will only work on the alphabet 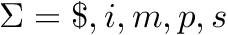$\Sigma = {\$, i, m, p, s}$ .

Implement a function std::vector<uint16_t> compute_count_table(std::string const & bwt) that returns a count table of length 5 with the counts for the characters $, i, m, p, s in that order.

Since we will often need the index of a given alphabet character, we will use the following helper function to map a character to an integer:

size_t to_index(char const chr)
{
    switch (chr)
    {
        case '$': return 0;
        case 'i': return 1;
        case 'm': return 2;
        case 'p': return 3;
        case 's': return 4;
        default: throw std::logic_error{"There is an illegal character in your text."};
    }
}

Given the following main function,

int main()
{
    std::string text{"mississippi"};
    std::string bwt = bwt_construction(text);
 
    // count table
    // -------------------------------------------------------------------------
    std::vector<uint16_t> count_table = compute_count_table(bwt);
 
    std::cout << "$ i m p s\n" << "---------\n";
    for (auto c : count_table)
        std::cout << c << " ";
    std::cout << '\n';
}

Your program should output the following:

$ i m p s
---------
0 1 5 6 8

If you are inexperienced with C++, you can use the following backbone:

Hint

std::vector<uint16_t> compute_count_table(std::string const & bwt)
{
    std::vector<uint16_t> count_table(5); // the prefix count table.
 
    for (auto chr : bwt)
    {
        // which positions in count_table need to be increased?
        for (size_t i = /*TODO: start position to be increased*/; i < /*TODO: end position to be increased*/; ++i)
            ++count_table[i]; // increase position i by 1.
    }
 
    return count_table;
}

Solution

std::vector<uint16_t> compute_count_table(std::string const & bwt)
{
    std::vector<uint16_t> count_table(5);
 
    for (auto chr : bwt)
    {
        for (size_t i = to_index(chr) + 1; i < 5; ++i)
            ++count_table[i];
    }
 
    return count_table;
}

Let $Occ : \Sigma \times [0..n] \rightarrow [0..n]$ be a function that maps $(c,k) \in \Sigma \times [0..n]$ to the number of occurrences of 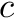in the prefix 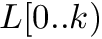of the transformed text .

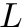If we would implement the occurrence table the naive way, i.e. via five arrays of length 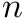of 64 bit integers for each character, we would need 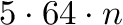$5 \cdot 64 \cdot n$ bits to store this array. In order to reduce the space consumption, we can introduce a more compact data structure:

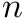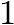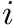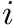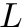We will use five Bitvectors of length , again one for each character, where we set a at position iff the corresponding character appears at position in . That way we only use 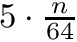$5 \cdot \frac{n}{64}$ bits of space if we use the bitvector implementation from the bitvector tutorial.

Implement the occurrence table via bitvectors

We will use the bitvector data structure from the previous bitvector tutorial. For simplicity, copy and paste the following code summary into a file called bitvector.hpp in your source directory. We will then be able to include the code into our current solution cpp file without any effort.

Since the occurrence table is a bit more complex, we will implement the occurrence functionality within a new struct.

#include "bitvector.hpp"
 
struct occurrence_table
{
    // The list of bitvectors:
    std::vector<Bitvector> data;
 
    // We want that 5 bitvectors are filled depending on the bwt,
    // so let's customise the constructor of occurrence_table:
    occurrence_table(std::string const & bwt)
    {
        // your code
    }
};

Implement the function the constructor that initialises the five bitvectors for the characters $, i, m, p, s. The bitvectors should have a 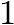set at position 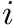iff the corresponding character appears at positio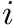n in 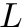(the bwt).

Given the following main function:

int main()
{
    std::string text{"mississippi"};
    std::string bwt = bwt_construction(text);
 
    // occurrence table
    // -------------------------------------------------------------------------
    occurrence_table Occ(bwt); // construction with bwt as the parameter
 
    std::cout << "   ";
    for (auto c : bwt)
        std::cout << c << " ";
    std::cout << "\n   -----------------------\n";
 
    std::string sigma{"$imps"};
    size_t s{};
    for (auto & bitv : Occ.data)
    {
        std::cout << sigma[s++] << "  ";
        for (size_t i = 0; i < bwt.size(); ++i)
            std::cout << bitv.read(i) << " ";
        std::cout << '\n';
    }
}

Your output should look like this:

   i p s s m $ p i s s i i
   -----------------------
$  0 0 0 0 0 1 0 0 0 0 0 0
i  1 0 0 0 0 0 0 1 0 0 1 1
m  0 0 0 0 1 0 0 0 0 0 0 0
p  0 1 0 0 0 0 1 0 0 0 0 0
s  0 0 1 1 0 0 0 0 1 1 0 0

If you are inexperienced with C++, you can use the following backbone:

Hint

#include "bitvector.hpp"
 
struct occurrence_table
{
    // The list of bitvectors:
    std::vector<Bitvector> data;
 
    // We want that 5 bitvectors are filled depending on the bwt,
    // so let's customise the constructor of occurrence_table:
    occurrence_table(std::string const & bwt)
    {
        // resize the 5 bitvectors to the length of the bwt:
        data.resize(/*TODO: How many Bitvectors?*/, Bitvector(/*TODO: How large should each bitvector be?*/));
 
        // fill the bitvectors
        for (size_t i = 0; i < bwt.size(); ++i)
            data[to_index(/* TODO: get the i'th character in the bwt.*/)].write(i, 1);
    }
};

Solution

struct occurrence_table
{
    // The list of bitvectors:
    std::vector<Bitvector> data;
 
    // We want that 5 bitvectors are filled depending on the bwt,
    // so let's customise the constructor of occurrence_table:
    occurrence_table(std::string const & bwt)
    {
        // resize the 5 bitvectors to the length of the bwt:
        data.resize(5, Bitvector(bwt.size()));
 
        // fill the bitvectors
        for (size_t i = 0; i < bwt.size(); ++i)
            data[to_index(bwt[i])].write(i, 1);
    }
};

Now when we use the occurrence table, we actually want to answer for example the query "How many characters 's' have I found up until position i in the bwt?".

This means we have to count number of 1's the bitvector for character 's' up until position i. Does this sound familiar? Indeed, it is a rank query. We have implemented rank support for our bitvector data structure in the bitvector tutorial so lets make use of this to implement access to the occurrence table.

Access the occurrence table

Adapt your constructor to also construct the helper data structures of your bitvector. Choose a block size of 3 bits and a superblock size of 6 bits (This is not recommended for real world data but serves as a toy example for the small bwt).
Implement the member function size_t read(char chr, size_t i) const that returns the number of occurrences of chr up until position i in the bwt using the rank support for the bitvectors.

Now given the following main function we can print the actual occurrence table:

int main()
{
    std::string text{"mississippi"};
    std::string bwt = bwt_construction(text);
 
    // occurrence table
    // -------------------------------------------------------------------------
    occurrence_table Occ(bwt); // construction with bwt as the parameter
 
    std::cout << "   ";
    for (auto c : bwt)
        std::cout << c << " ";
    std::cout << "\n   -----------------------\n";
 
    std::string sigma{"$imps"};
    for (auto chr : sigma)
    {
        std::cout << chr << "  ";
        for (size_t i = 0; i < bwt.size(); ++i)
            std::cout << Occ.read(chr, i) << " ";
        std::cout << '\n';
    }
}

The output should look like this:

   i p s s m $ p i s s i i
   -----------------------
$  0 0 0 0 0 1 1 1 1 1 1 1
i  1 1 1 1 1 1 1 2 2 2 3 4
m  0 0 0 0 1 1 1 1 1 1 1 1
p  0 1 1 1 1 1 2 2 2 2 2 2
s  0 0 1 2 2 2 2 2 3 4 4 4

If you are inexperienced with C++, you can use the following backbone:

Hint

struct occurrence_table
{
    // The list of bitvectors:
    std::vector<Bitvector> data;
 
    // We want that 5 bitvectors are filled depending on the bwt,
    // so let's customise the constructor of occurrence_table:
    occurrence_table(std::string const & bwt)
    {
        // resize the 5 bitvectors to the length of the bwt:
        data.resize(5, Bitvector(bwt.size()));
 
        // fill the bitvectors
        for (size_t i = 0; i < bwt.size(); ++i)
            data[to_index(bwt[i])].write(i, 1);
 
        // construct the helper data structures
        for (Bitvector & bitv : data)
            /*TODO: Call the construct member function with block size 3 and superblock size 6*/;
    }
 
    bool read(char const chr, size_t const i) const
    {
        return /*TODO: For the bitvector corresponding to chr in data, call the rank member function at position i + 1*/;
    }
};

Solution

struct occurrence_table
{
    // The list of bitvectors:
    std::vector<Bitvector> data;
 
    // We want that 5 bitvectors are filled depending on the bwt,
    // so let's customise the constructor of occurrence_table:
    occurrence_table(std::string const & bwt)
    {
        // resize the 5 bitvectors to the length of the bwt:
        data.resize(5, Bitvector(bwt.size()));
 
        // fill the bitvectors
        for (size_t i = 0; i < bwt.size(); ++i)
            data[to_index(bwt[i])].write(i, 1);
 
        for (Bitvector & bitv : data)
            bitv.construct(3, 6);
    }
 
    size_t read(char const chr, size_t const i)
    {
        return data[to_index(chr)].rank(i + 1);
    }
};

Backward Search

Now that we have the helper data structures, we can conduct an efficient pattern search within our bwt.

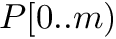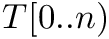The pseudo code to compute the number of occurrences of a pattern in is the following:

(1)  count(P[0..m-1])
(2)  i = m - 1, a = 0, b = n - 1;
(3)  while ((a <= b) AND (i >= 0)) do
(4)      c = P[i];
(5)      a = C(c) + Occ(c, a - 1)
(6)      b = C(c) + Occ(c, b) - 1;
(7)      i = i - 1;
(8)
(9)  if (b < a) then return not found;
(10) else return found (b - a + 1) occurrences;

Backward search

Using all of your code so far, implement a function

size_t count(std::string const & P,
             std::string const & bwt,
             std::vector<uint16_t> const & C,
             occurrence_table const & Occ)
{
    // your code goes here
}

that returns the number of occurrences of pattern P.

Given the following main function:

int main()
{
    std::string text{"mississippi"};
 
    // compute the bwt, C and Occ:
    std::string bwt = bwt_construction(text);
    std::vector<uint16_t> C = compute_count_table(bwt);
    occurrence_table Occ(bwt);
 
    std::cout << count("ssi", bwt, C, Occ) << '\n'; // prints 2
    std::cout << count("ppi", bwt, C, Occ) << '\n'; // prints 1
}

Your program should output

2

1

If you are inexperienced with C++, you can use the following backbone:

Hint

size_t count(std::string const & P,
             std::string const & bwt,
             std::vector<uint16_t> const & C,
             occurrence_table const & Occ)
{
    int64_t i = /*TODO: where do we start our search in the pattern?*/;
    size_t a =  /*TODO: what is the lower bound to start?*/;
    size_t b =  /*TODO: what is the upper bound to start?*/;
 
    while ((a <= b) && (i >= 0))
    {
        char c = /*TODO: The character at position i in P.*/;
 
        // Note that () ? x : y in the next line takes care of the case that a is 0
        // because a - 1 would be negative and Occ.read at a negative position is invalid.
        a = /*TODO: C at the index of c*/ + (a ? Occ.read(c, a - 1) : 0);
 
        b = /*TODO: C at the index of c*/ +  /*TODO: read Occ at position b with character c*/ - 1;
 
        i = i - 1;
    }
 
    if (b < a)
        return 0;
    else
        return (b - a + 1);
}

Solution

size_t count(std::string const & P,
             std::string const & bwt,
             std::vector<uint16_t> const & C,
             occurrence_table const & Occ)
{
    int64_t i = P.size() - 1;
    size_t a = 0;
    size_t b = bwt.size() - 1;
 
    while ((a <= b) && (i >= 0))
    {
        char c = P[i];
        a = C[to_index(c)] + (a ? Occ.read(c, a - 1) : 0);
        b = C[to_index(c)] + Occ.read(c, b) - 1;
 
        i = i - 1;
    }
 
    if (b < a)
        return 0;
    else
        return (b - a + 1);
}

Here is the full solution in case you need it:

Solution

#include <algorithm>
#include <iostream>
#include <numeric>
#include <string>
#include <vector>
 
#include "bitvector.hpp"
 
std::string bwt_construction(std::string const & text)
{
    std::string bwt{};
 
    std::vector<uint64_t> sa(text.size() + 1);
    std::iota(sa.begin(), sa.end(), 0);
    std::sort(sa.begin(), sa.end(), [&text](uint64_t a, uint64_t b) -> bool
    {
        while (a < text.size() && b < text.size() && text[a] == text[b])
        {
            ++a, ++b;
        }
 
        if (b == text.size())
            return false;
 
        if (a == text.size())
            return true;
 
        return text[a] < text[b];
    });
 
    for (auto x : sa)
    {
        if (!x)
            bwt += "$";
        else
            bwt += text[x-1];
    }
 
    return bwt;
}
 
size_t to_index(char const chr)
{
    switch (chr)
    {
        case '$': return 0;
        case 'i': return 1;
        case 'm': return 2;
        case 'p': return 3;
        case 's': return 4;
        default: throw std::logic_error{"There is an illegal character in your text."};
    }
}
 
std::vector<uint16_t> compute_count_table(std::string const & bwt)
{
    std::vector<uint16_t> count_table(5);
 
    for (auto chr : bwt)
    {
        for (size_t i = to_index(chr) + 1; i < 5; ++i)
            ++count_table[i];
    }
 
    return count_table;
}
 
struct occurrence_table
{
    // The list of bitvectors:
    std::vector<Bitvector> data;
 
    // We want that 5 bitvectors are filled depending on the bwt,
    // so let's customise the constructor of occurrence_table:
    occurrence_table(std::string const & bwt)
    {
        // resize the 5 bitvectors to the length of the bwt:
        data.resize(5, Bitvector(bwt.size()));
 
        // fill the bitvectors
        for (size_t i = 0; i < bwt.size(); ++i)
            data[to_index(bwt[i])].write(i, 1);
 
        for (Bitvector & bitv : data)
            bitv.construct(3, 6);
    }
 
    size_t read(char const chr, size_t const i) const
    {
        return data[to_index(chr)].rank(i + 1);
    }
};
 
size_t count(std::string const & P,
             std::string const & bwt,
             std::vector<uint16_t> const & C,
             occurrence_table const & Occ)
{
    int64_t i = P.size() - 1;
    size_t a = 0;
    size_t b = bwt.size() - 1;
 
    while ((a <= b) && (i >= 0))
    {
        char c = P[i];
        a = C[to_index(c)] + (a ? Occ.read(c, a - 1) : 0);
        b = C[to_index(c)] + Occ.read(c, b) - 1;
 
        i = i - 1;
    }
 
    if (b < a)
        return 0;
    else
        return (b - a + 1);
}
 
int main()
{
    std::string text{"mississippi"};
 
    // compute the bwt, C and Occ:
    std::string bwt = bwt_construction(text);
    std::vector<uint16_t> C = compute_count_table(bwt);
    occurrence_table Occ(bwt);
 
    std::cout << count("ssi", bwt, C, Occ) << '\n'; // prints 2
    std::cout << count("ppi", bwt, C, Occ) << '\n'; // prints 1
}

Real data example with SeqAn3

In the following section, we will conduct a search in an FM-index using SeqAn3. We will search for 1'000'000 reads within chr4 of the Drosophila genome and count how many reads occur more than 100 times, indicating a repeat region!

Download the following data for this example:

reference file
query file into the tutorial directory.

As a first step, set up SeqAn3 by following the Setup tutorial and add an executable count_occurrences to the CMakeLists.txt. Create a new file count_occurrences.cpp in the source directory with the following content:

#include <iostream>
 
#include <seqan3/io/sequence_file/all.hpp>
#include <seqan3/search/all.hpp>
 
int main()
{
    seqan3::sequence_file_input reference_in{file_path_to_reference}; // Read the reference (only 1 contig).
    seqan3::sequence_file_input query_in{file_path_to_reference}; // Read the query file (multiple contigs).
 
     // Create an FM-index from the reference (first record).
    seqan3::fm_index index{(*reference_in.begin()).sequence()};
 
    size_t counter{0u};
 
    for (auto & rec : query_in) // For each record in our query file
    {
        // search the query sequence in the index with seqan3::search
        auto res = seqan3::search(rec.sequence(), index);
 
        if (std::ranges::distance(res) > 100) // if more than 100 hits were found
            ++counter;                        // increase the counter
    }
 
    seqan3::debug_stream << "Found " << counter << " queries with more than 100 exact hits.\n";
}

The above code basically does the same things as you just implemented in this nanocourse. The SeqAn library provides a lot of commonly needed functionality when working with high throughput sequencing, such that you do not need to implement your own data structures and algorithms.

We use the sequence_file_input to handle reference and read input - the format and content of the files is taken care of automatically. The fm_index encapsulates a suffix array, occurrence table and count table just like we implemented it ourselves before. By calling search we can compute every position that a query matches the index; unless configured in another way, this will report every exact hit within our reference.

Run cmake -DCMAKE_CXX_FLAGS="-O3 -march=native" ../source within the build directory and execute the program via ./count_occurrences and measure runtime and memory consumption via, for example, /usr/bin/time -v ./count_occurrences.

If you want to learn more about SeqAn3, we recommend you start with the tutorials.

Difficulty	Easy
Duration	120 min
Prerequisite tutorials	Compact Data Structures - Bitvectors
Recommended reading	Compact Data Structures (Navarro)

Table of Contents

Motivation

Theoretical Background: Burrows-Wheeler transform and LF-Mapping

Helper data structures: Occ & C

Implement the count table

Implement the occurrence table via bitvectors

Access the occurrence table

Backward Search

Backward search

Real data example with SeqAn3